Zadanie nr 9287471
Gracz 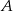 rzuca raz sześcienną kostką z liczbami 2,4 i 9 na ściankach, a gracz
rzuca raz sześcienną kostką z liczbami 2,4 i 9 na ściankach, a gracz 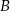 rzuca raz kostką z liczbami 3,5 i 7 przy czym każda liczba znajduje się na dwóch ściankach kostki. Wygrywa ten gracz, na którego kostce wypadnie większa liczba. Oblicz prawdopodobieństwo wygrania gracza
rzuca raz kostką z liczbami 3,5 i 7 przy czym każda liczba znajduje się na dwóch ściankach kostki. Wygrywa ten gracz, na którego kostce wypadnie większa liczba. Oblicz prawdopodobieństwo wygrania gracza 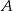 .
.
Rozwiązanie
Sposób I
Jeżeli za zdarzenia elementarne przyjmiemy pary otrzymanych wyników, to mamy
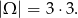
Zdarzenia sprzyjające są następujące:
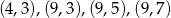
Zatem prawdopodobieństwo wynosi
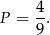
Sposób II
Każdy wynik u każdego z graczy wypada z prawdopodobieństwem
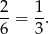
Aby 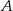 wygrał musi wyrzucić 4 lub 9. Jeżeli wyrzuci 4, to
wygrał musi wyrzucić 4 lub 9. Jeżeli wyrzuci 4, to 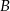 musi wyrzucić 3. Prawdopodobieństwo takiego zdarzenia to
musi wyrzucić 3. Prawdopodobieństwo takiego zdarzenia to
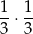
(można myśleć, że to wzór na prawdopodobieństwo warunkowe niezależnych zdarzeń, czyli wzór typu 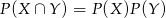 ; lub narysować sobie drzewko).
; lub narysować sobie drzewko).
Jeżeli 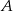 wyrzuci
wyrzuci 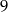 to każdy wynik
to każdy wynik 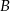 daje
daje 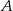 wygraną, zatem prawdopodobieństwo takiej sytuacji to
wygraną, zatem prawdopodobieństwo takiej sytuacji to
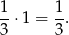
Szukane prawdopodobieństwo wynosi więc
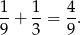
Odpowiedź: 

