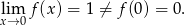Zadanie nr 2349903
Dana jest funkcja
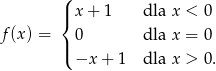
Wykaż, że funkcja ta nie jest ciągła w punkcie 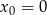 .
.
Rozwiązanie
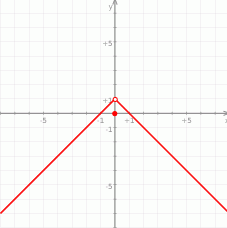
Musimy sprawdzić, że 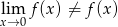 . Jak się narysuje wykres to jest to dość oczywiste, ale możemy też policzyć
. Jak się narysuje wykres to jest to dość oczywiste, ale możemy też policzyć
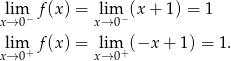
Czyli
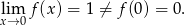
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dana jest funkcja
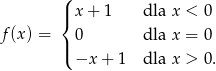
Wykaż, że funkcja ta nie jest ciągła w punkcie 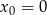 .
.
Musimy sprawdzić, że 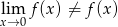 . Jak się narysuje wykres to jest to dość oczywiste, ale możemy też policzyć
. Jak się narysuje wykres to jest to dość oczywiste, ale możemy też policzyć
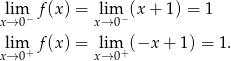
Czyli