Zadanie nr 2563220
Uzasadnij, że nie istnieje granica 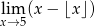 .
.
Rozwiązanie
Liczymy granice jednostronne
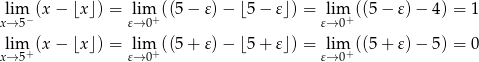
Ponieważ granice jednostronne są różne, podana granica nie istnieje.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Uzasadnij, że nie istnieje granica 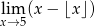 .
.
Liczymy granice jednostronne
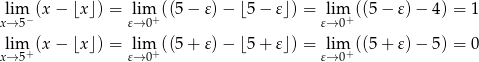
Ponieważ granice jednostronne są różne, podana granica nie istnieje.
