Zadanie nr 2906554

Wyznacz równania wszystkich stycznych do wykresu funkcji 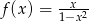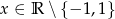-x-- f(x) = 1−x2 , x ∈ R ∖{ − 1,1} nachylonych do osi 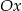pod kątem 45∘ .

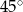Rozwiązanie

Jeżeli styczna ma być nachylona do osi 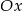pod kątem 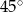∘ 4 5 , to musi mieć współczynnik kierunkowy równy 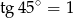tg 45∘ = 1 . Liczymy pochodną danej funkcji

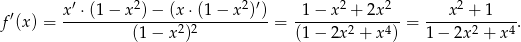
′ x′ ⋅(1-−-x-2)−-(x-⋅(1-−-x2)′) -1−-x-2 +-2x-2- ----x2 +-1--- f (x ) = (1 − x 2)2 = (1− 2x 2 + x4) = 1 − 2x 2 + x4.

Sprawdzamy teraz, kiedy pochodna jest równa 1.

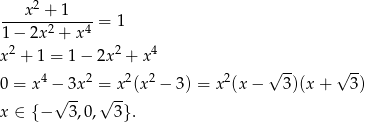
2 ---x--+-1----= 1 1 − 2x 2 + x 4 x2 + 1 = 1 − 2x 2 + x 4 √ -- √ -- 0 = x 4 − 3x 2 = x2(x2 − 3) = x 2(x− 3)(x+ 3) √ -- √ -- x ∈ {− 3,0 , 3}.

Widać, że są trzy takie punkty. Obliczamy jeszcze wartość funkcji w każdym z tych punktów.

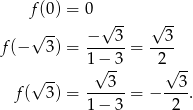
f(0) = 0 √ -- √ -- √ -- f(− 3) = −--3-= --3- 1√− 3- 2√ -- √ -- 3 3 f( 3) = -----= − ----. 1− 3 2

Otrzymujemy więc następujące trzy równania stycznych

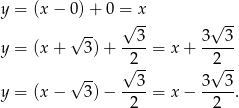
y = (x − 0) + 0 = x √ -- √ 3- 3√ 3- y = (x + 3) + ----= x + ----- √2-- √2-- √ -- 3 3 3 y = (x − 3) − -2--= x − --2--.

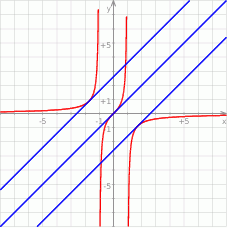
Na koniec, dla ciekawskich, wykres całej sytuacji.

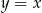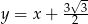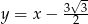Odpowiedź: y = x , √- y = x + 323- , √- y = x− 323- .