Zadanie nr 3547558
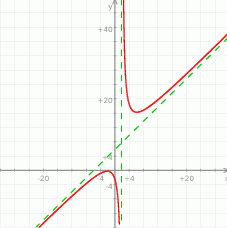
Określ dziedzinę i wyznacz równania wszystkich asymptot wykresu funkcji 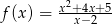 .
.
Rozwiązanie
Dziedziną jest zbiór 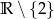 . Jeżeli zapiszemy wzór funkcji w postaci
. Jeżeli zapiszemy wzór funkcji w postaci
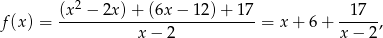
to widać, że dla 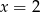 mamy asymptotę pionową (granice
mamy asymptotę pionową (granice 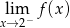 i
i 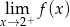 są niewłaściwe). Jednocześnie widać, że nie ma asymptot poziomych, bo
są niewłaściwe). Jednocześnie widać, że nie ma asymptot poziomych, bo 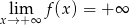 i
i 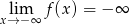 . Pozostało sprawdzić czy nie ma asymptot ukośnych. Najpierw liczymy granice
. Pozostało sprawdzić czy nie ma asymptot ukośnych. Najpierw liczymy granice
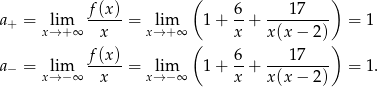
Teraz liczymy granice
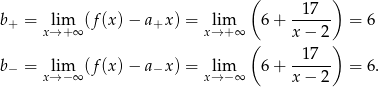
Jest zatem jedna asymptota ukośna 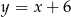 .
.
Na koniec, dla ciekawskich, wykres funkcji 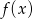 .
.
Odpowiedź: 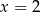 i
i