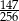Zadanie nr 3576387
Oblicz pole trójkąta ograniczonego przez osie układu współrzędnych oraz styczną do wykresu funkcji 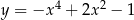 w punkcie
w punkcie 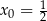 .
.
Rozwiązanie
Liczymy pochodną danej funkcji
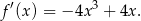
Współczynnik kierunkowy stycznej w punkcie 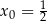 jest równy
jest równy
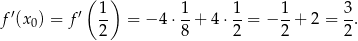
Styczna ma więc postać 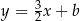 . Współczynnik
. Współczynnik 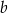 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu
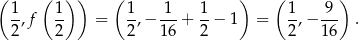
Mamy zatem
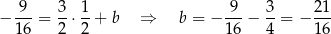
Styczna ma więc równanie 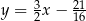 . Jej punkt przecięcia z osią
. Jej punkt przecięcia z osią 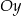 to
to 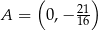 . Wyznaczmy jeszcze jej punkt przecięcia z osią
. Wyznaczmy jeszcze jej punkt przecięcia z osią 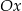 .
.
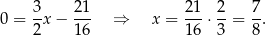
Punkt przecięcia  stycznej z osią
stycznej z osią 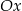 ma więc współrzędne
ma więc współrzędne 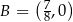 .
.
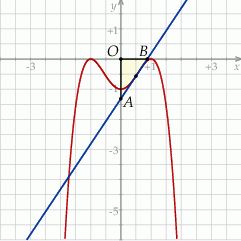
Pole trójkąta 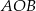 jest więc równe
jest więc równe
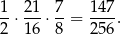
Odpowiedź: