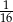/Studia/Analiza/Funkcje/Badanie funkcji

Zadanie nr 3637845

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz granicę 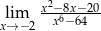x2−-8x−-20 xli→m−2 x6−64 .

Rozwiązanie

Łatwo sprawdzić, że zarówno licznik jak i mianownik zerują się dla 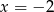x = − 2 , więc oba muszą dzielić się przez 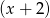(x + 2) . Rozkładamy trójmian w liczniku.

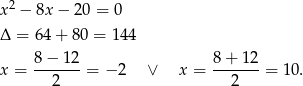
x2 − 8x − 2 0 = 0 Δ = 64 + 80 = 1 44 x = 8−--12-= − 2 ∨ x = 8-+-12-= 10. 2 2

Mamy zatem (korzystamy ze wzorów na różnicę kwadratów i sześcianów).

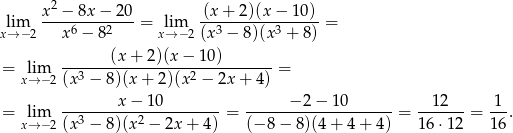
2 lim x-−--8x-−-20-= lim -(x+--2)(x-−-10)-= x→ −2 x6 − 82 x→ −2(x 3 − 8 )(x 3 + 8) = lim ------(x-+-2)(x-−-1-0)-------= x→ −2 (x3 − 8)(x+ 2)(x2 − 2x + 4) x − 10 −2 − 1 0 12 1 = lim --3-------2-----------= --------------------= -------= ---. x→ −2 (x − 8)(x − 2x + 4) (− 8− 8)(4+ 4+ 4) 16 ⋅12 16

 
Odpowiedź: -1 16

Wersja PDF