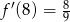Zadanie nr 3696764
Funkcja 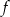 jest określona wzorem
jest określona wzorem 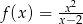 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 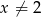 . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 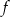 w punkcie
w punkcie 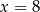 .
.
Rozwiązanie
Korzystamy ze wzoru na pochodną ilorazu
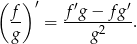
Liczymy
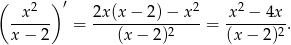
Mamy zatem
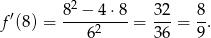
Odpowiedź: 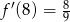
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Funkcja 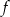 jest określona wzorem
jest określona wzorem 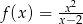 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 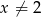 . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 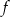 w punkcie
w punkcie 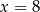 .
.
Korzystamy ze wzoru na pochodną ilorazu
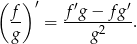
Liczymy
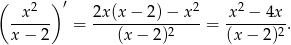
Mamy zatem
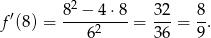
Odpowiedź: