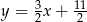/Studia/Analiza/Funkcje/Badanie funkcji

Zadanie nr 3950016

Dodaj do ulubionych
Dodaj do rozwiązanych

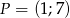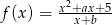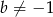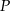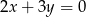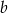Punkt P = (1;7) należy do wykresu funkcji x2+ax-+5- f(x) = x+b , gdzie b ⁄= − 1 . Styczna do wykresu danej funkcji, poprowadzona w punkcie P , jest prostopadła do prostej o równaniu 2x + 3y = 0 . Oblicz współczynniki a i b oraz napisz równanie tej stycznej.

Rozwiązanie

Na początku wykorzystajmy informację o tym, że punkt 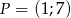P = (1;7 ) należy do wykresu funkcji.

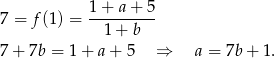
7 = f (1) = 1-+-a-+-5 1 + b 7 + 7b = 1+ a + 5 ⇒ a = 7b + 1.

Zatem funkcja ma wzór

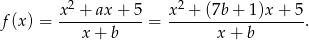
x2 + ax + 5 x2 + (7b + 1)x + 5 f(x) = ------------= ------------------. x + b x + b

Współczynnik kierunkowy stycznej w punkcie 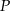P to dokładnie 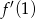f ′(1) , obliczymy zatem pochodną ′ f (x) .

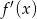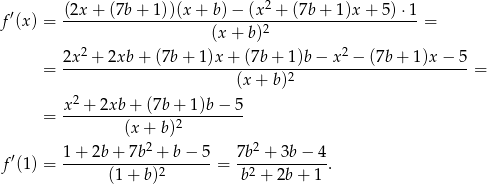
(2x + (7b + 1))(x+ b)− (x2 + (7b+ 1)x+ 5)⋅1 f′(x) = -------------------------------------------------= (x + b )2 2x 2 + 2xb + (7b+ 1)x + (7b + 1)b − x2 − (7b + 1)x − 5 = -------------------------------2------------------------= (x + b) x 2 + 2xb + (7b+ 1)b− 5 = ---------(x-+--b)2-------- ′ 1-+-2b-+-7b-2 +-b-−-5 7b2-+-3b-−-4- f (1) = (1 + b)2 = b2 + 2b + 1 .

Z drugiej strony wiemy, że styczna ta jest prostopadła do prostej

y = − 2x, 3

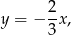
zatem jej współczynnik kierunkowy jest równy 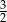32 . Daje to nam równanie

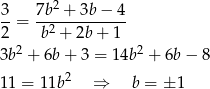
2 3-= 7b-+--3b−--4- 2 b2 + 2b + 1 3b2 + 6b+ 3 = 14b2 + 6b − 8 11 = 11b2 ⇒ b = ± 1

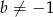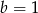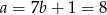Ponieważ z założenia b ⁄= −1 , mamy b = 1 i a = 7b+ 1 = 8 .

Szukana styczna jest postaci 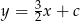y = 3x + c 2 . Współczynnik c wyliczamy z faktu, że ta styczna przechodzi przez punkt P(1 ;7) .

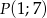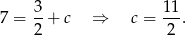
3 11 7 = --+ c ⇒ c = --. 2 2

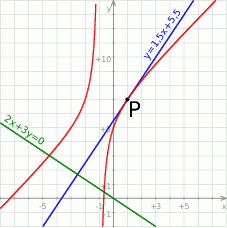
Na koniec, dla ciekawskich, obrazek całej sytuacji.

PIC

 
Odpowiedź: 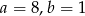a = 8,b = 1 , styczna: y = 3x + 11 2 2

Wersja PDF