/Studia/Analiza/Funkcje/Badanie funkcji

Zadanie nr 4374631

Dodaj do ulubionych
Dodaj do rozwiązanych

Zbadaj przebieg zmienności funkcji 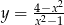4−x-2 y = x2− 1 .

Rozwiązanie

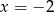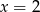Miejsca zerowe funkcji to x = − 2 i x = 2 . Funkcja jest parzysta: f (−x ) = f(x) .

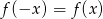Zacznijmy od asymptot.

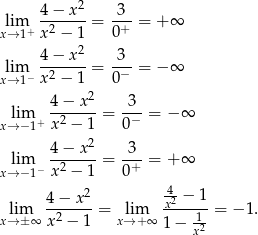
4-−-x2- 3-- xl→im1+ x2 − 1 = 0+ = + ∞ 2 lim 4-−-x--= 3--= − ∞ x→ 1− x2 − 1 0− 4 − x 2 3 lim --2----= -−- = − ∞ x→ − 1+x − 1 0 4 − x 2 3 lim −--2----= -+- = + ∞ x→ − 1 x − 1 0 4− x2 4x2 − 1 x→lim± ∞ -2-----= x→lim+ ∞ ----1--= − 1. x − 1 1− x2

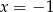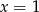Zatem funkcja ma asymptoty pionowe x = − 1 i x = 1 oraz asymptotę poziomą y = − 1 .

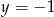Zbadajmy teraz monotoniczność i wypukłość funkcji.

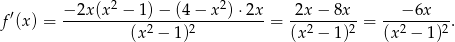
′ − 2x (x2 − 1)− (4− x2)⋅2x 2x − 8x −6x f (x) = ----------(x2 −-1)2--------- = (x-2 −-1-)2 = (x2-−-1)2.

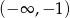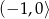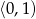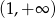Widać stąd, że funkcja jest rosnąca na przedziałach (− ∞ ,− 1) i (− 1,0⟩ (bo pochodna jest dodatnia), malejąca na przedziałach ⟨0,1) i (1,+ ∞ ) (pochodna jest ujemna), oraz ma maksimum lokalne w punkcie 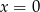x = 0 (pochodna zmienia znak z ’+’ na ’-’).

Teraz badamy wypukłość

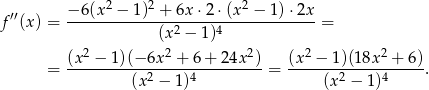
′′ −-6(x2 −-1)2 +-6x-⋅2⋅(x-2 −-1-)⋅2x f (x) = (x2 − 1)4 = 2 2 2 2 2 = (x-−--1)(−-6x--+-6+--24x-)-= (x--−-1)(18x--+-6)-. (x 2 − 1 )4 (x2 − 1)4

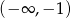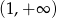Widać teraz, że funkcja jest wypukła na przedziałach (− ∞ ,− 1) i (1,+ ∞ ) (druga pochodna dodatnia) oraz wklęsła na 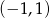(− 1,1) (druga pochodna ujemna). Nie ma punktów przegięcia.

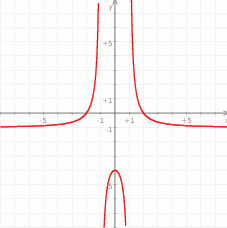
Teraz bez trudu rysujemy wykres funkcji.

PIC

Wersja PDF