Zadanie nr 5021877
Dla jakich wartości parametru 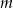 granica funkcji
granica funkcji 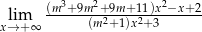 jest równa czwartemu wyrazowi ciągu określonego wzorem rekurencyjnym
jest równa czwartemu wyrazowi ciągu określonego wzorem rekurencyjnym 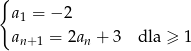
Rozwiązanie
Liczymy daną granicę – dzielimy licznik i mianownik przez 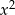 .
.
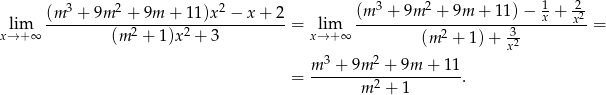
Obliczamy 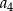
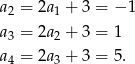
Pozostało więc rozwiązać równanie
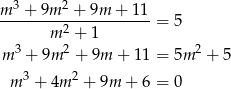
Szukamy teraz pierwiastków całkowitych tego równania – sprawdzamy dzielniki wyrazu wolnego. Jednym z nich 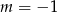 , więc dzielimy wielomian przez
, więc dzielimy wielomian przez 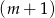 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
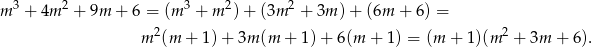
Trójmian w drugim nawiasie nie ma pierwiastków (bo 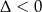 ), więc jedyną wartością
), więc jedyną wartością 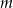 jest
jest 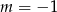 .
.
Odpowiedź: