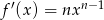Zadanie nr 5888941
Oblicz z definicji pochodną funkcji 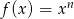 , gdzie
, gdzie 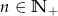 .
.
Rozwiązanie
Korzystamy ze wzoru skróconego mnożenia
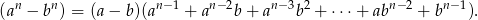
Liczymy pochodną w punkcie 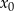 .
.
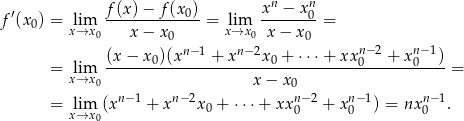
Odpowiedź: 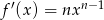
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz z definicji pochodną funkcji 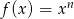 , gdzie
, gdzie 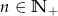 .
.
Korzystamy ze wzoru skróconego mnożenia
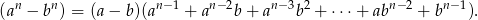
Liczymy pochodną w punkcie 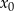 .
.
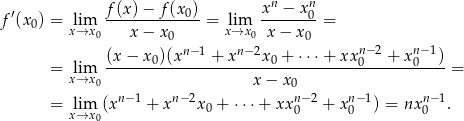
Odpowiedź: