/Studia/Analiza/Funkcje/Badanie funkcji

Zadanie nr 7365061

Dodaj do ulubionych
Dodaj do rozwiązanych

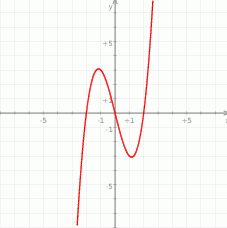
Zbadaj przebieg zmienności funkcji 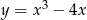3 y = x − 4x .

Rozwiązanie

Ponieważ

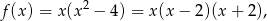
2 f(x) = x (x − 4) = x(x − 2)(x + 2 ),

więc miejscami zerowymi funkcji są liczby 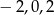− 2,0,2 . Funkcja jest nieparzysta.

Ponieważ jest to wielomian, nie ma asymptot, więc przechodzimy do badania monotoniczności.

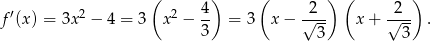
( ) ( ) ( ) ′ 2 2 4- -2-- -2-- f(x ) = 3x − 4 = 3 x − 3 = 3 x − √ 3- x + √ 3- .

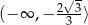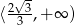Widzimy zatem, że funkcja jest rosnąca na przedziałąch 2√3 (− ∞ ,− -3-⟩ i √ - ⟨2--3,+ ∞ ) 3 (pochodna dodatnia), oraz malejąca na przedziale 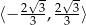√ - √ - ⟨− 2-3, 2-3⟩ 3 3 (pochodna jest ujemna). W punkcie 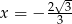√- x = − 233- jest maksimum lokalne, a w punkcie 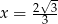2√-3- x = 3 minimum lokalne.

Zbadajmy jeszcze wypukłość.

′′ f (x ) = 6x.

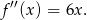
Zatem funkcja jest wypukła na przedziale 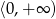⟨0,+ ∞ ) (druga pochodna dodatnia) i wklęsła na przedziale 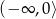(− ∞ ,0⟩ (druga pochodna ujemna). W punkcie 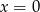x = 0 jest punkt przegięcia (druga pochodna zmienia znak).

Teraz bez trudu szkicujemy wykres.

PIC

Wersja PDF