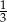Zadanie nr 8191052
Oblicz granicę 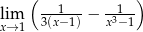 .
.
Rozwiązanie
Liczymy
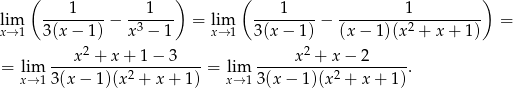
Zanim przekształcimy to wyrażenie dalej, rozłóżmy trójmian w liczniku na czynniki.
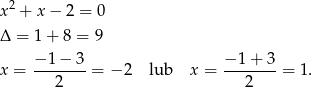
Zatem 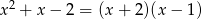 i interesującą nas granicę możemy przekształcić następująco.
i interesującą nas granicę możemy przekształcić następująco.
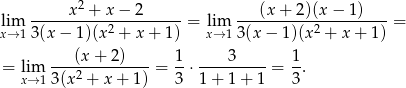
Odpowiedź: 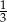
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz granicę 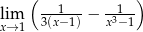 .
.
Liczymy
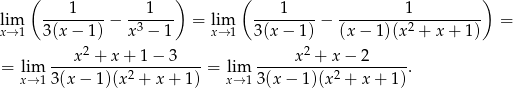
Zanim przekształcimy to wyrażenie dalej, rozłóżmy trójmian w liczniku na czynniki.
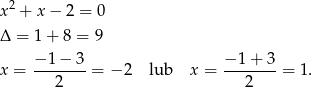
Zatem 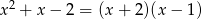 i interesującą nas granicę możemy przekształcić następująco.
i interesującą nas granicę możemy przekształcić następująco.
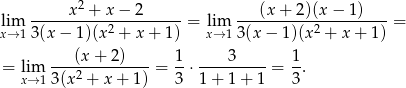
Odpowiedź: