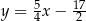/Studia/Analiza/Funkcje/Badanie funkcji

Zadanie nr 8289629

Dodaj do ulubionych
Dodaj do rozwiązanych

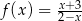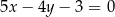Napisz równanie stycznych do wykresu funkcji x+3- f(x) = 2−x i równoległych do prostej o równaniu 5x − 4y − 3 = 0 .

Rozwiązanie

Daną prostą możemy zapisać w postaci

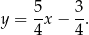
5 3 y = --x − -. 4 4

Musimy znaleźć punkty na hiperboli, w których styczna ma współczynnik kierunkowy 5 4 . Współczynnik kierunkowy stycznej w punkcie to dokładnie pochodna w tym punkcie. Liczymy pochodną

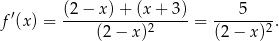
f′(x) = (2-−-x-)+-(x-+-3-)= ----5----. (2− x)2 (2 − x)2

Sprawdzamy kiedy pochodna równa się 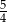54 .

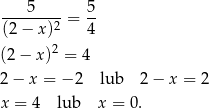
---5-----= 5- (2− x)2 4 2 (2− x ) = 4 2− x = − 2 lub 2− x = 2 x = 4 lub x = 0 .

Liczymy jeszcze wartości funkcji w tych punktach

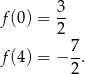
3 f(0 ) = -- 2 f(4 ) = − 7. 2

Są więc dwie styczne spełniające warunki zadania.

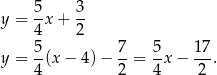
5 3 y = -x + -- 4 2 y = 5(x − 4) − 7-= 5x − 17. 4 2 4 2

Na koniec, dla ciekawskich, wykres całej sytuacji.

PIC

 
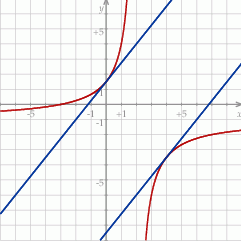
Odpowiedź: 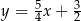y = 54x + 32 i y = 54x − 172

Wersja PDF