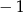Zadanie nr 8408490
Oblicz granicę 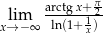 .
.
Rozwiązanie
Ponieważ mamy symbol nieoznaczony ![0 [0]](https://img.zadania.info/zad/8408490/HzadR0x.gif) , liczymy z twierdzenia de l’Hospitala.
, liczymy z twierdzenia de l’Hospitala.
![π π --1- arctg-x-+--2-[H ] (arctg-x+--2)′ ---1+x-2---- xl→im−∞ ln (1+ 1) = xl→im−∞ (ln(1 + 1))′ = x→lim− ∞ -1--⋅(− -1) = x x 1+1x x2 -1-- 2 x2+x- = lim --1+x-2- = − lim x--+-x-= − lim --x2- = x→ −∞ − 21--- x→ − ∞ 1 + x2 x→ −∞ 1+x-2 x+x x2 1-+-1x-- = − x→lim− ∞ 1- = − 1. x2 + 1](https://img.zadania.info/zad/8408490/HzadR1x.gif)
Odpowiedź: 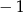
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz granicę 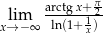 .
.
Ponieważ mamy symbol nieoznaczony ![0 [0]](https://img.zadania.info/zad/8408490/HzadR0x.gif) , liczymy z twierdzenia de l’Hospitala.
, liczymy z twierdzenia de l’Hospitala.
![π π --1- arctg-x-+--2-[H ] (arctg-x+--2)′ ---1+x-2---- xl→im−∞ ln (1+ 1) = xl→im−∞ (ln(1 + 1))′ = x→lim− ∞ -1--⋅(− -1) = x x 1+1x x2 -1-- 2 x2+x- = lim --1+x-2- = − lim x--+-x-= − lim --x2- = x→ −∞ − 21--- x→ − ∞ 1 + x2 x→ −∞ 1+x-2 x+x x2 1-+-1x-- = − x→lim− ∞ 1- = − 1. x2 + 1](https://img.zadania.info/zad/8408490/HzadR1x.gif)
Odpowiedź: