Zadanie nr 8826301
Oblicz pochodną funkcji 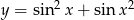 .
.
Rozwiązanie
Korzystamy ze wzoru na pochodną złożenia.
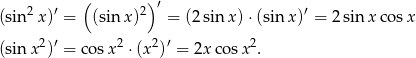
Zatem
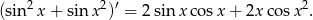
Odpowiedź: 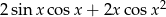
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz pochodną funkcji 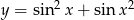 .
.
Korzystamy ze wzoru na pochodną złożenia.
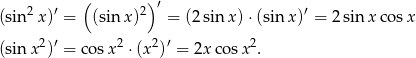
Zatem
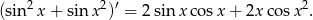
Odpowiedź: