/Studia/Analiza/Funkcje/Badanie funkcji

Zadanie nr 9012579

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz granicę 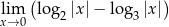( ) lxim→ 0 log2|x| − log3|x| .

Rozwiązanie

Ponieważ 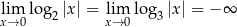lxi→m0log2 |x | = lix→m0 log 3|x| = − ∞ , musimy wyrażenie pod granicą odrobinę przekształcić, zanim będzie widać, jaki jest wynik. Korzystamy ze wzoru

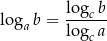
lo gcb loga b = ------ lo gca

na zmianę podstawy logarytmu. Mamy zatem

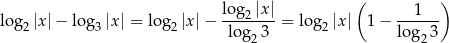
lo g |x| ( 1 ) log2|x| − log3|x| = log 2|x|− ---2----= log2 |x | 1− ------ log 23 lo g23

Teraz wystarczy zauważyć że

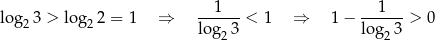
--1--- --1--- log2 3 > lo g22 = 1 ⇒ log 3 < 1 ⇒ 1− lo g 3 > 0 2 2

oraz

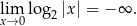
lim log 2|x| = − ∞ . x→ 0

Stąd

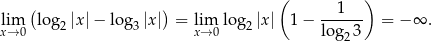
( ) lim (log |x|− log |x|) = lim log |x| 1 − ---1-- = − ∞ . x→ 0 2 3 x→ 0 2 log 23

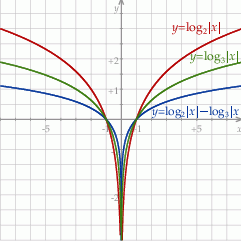
Na koniec wykresy pojawiających się wyżej funkcji.

PIC

 
Odpowiedź: − ∞

Wersja PDF