/Studia/Analiza/Funkcje/Badanie funkcji

Zadanie nr 9541844

Dodaj do ulubionych
Dodaj do rozwiązanych

Uzasadnij, że funkcja 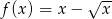√ -- f (x) = x − x jest różnowartościowa na zbiorze [14;+ ∞ ) .

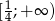Rozwiązanie

Musimy pokazać, że jeżeli 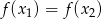f(x1) = f(x 2) dla pewnych 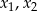x1,x2 z dziedziny to x1 = x2 .

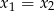Liczymy (korzystamy ze wzoru 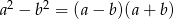a2 − b2 = (a − b)(a + b) )

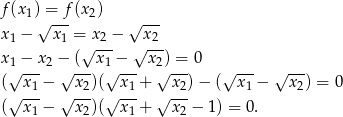
f(x1) = f(x 2) x − √x--= x − √x--- 1 1 √ 2-- √ 2-- x1 −-x2 − (--x1 −-- x2) =-0 --- --- (√ x1 − √ x2)(√ x1 + √ x2)− (√ x1 − √ x2) = 0 √ --- √ --- √ --- √ --- ( x1 − x2)( x1 + x2 − 1) = 0.

Jeżeli pierwszy nawias jest zero to koniec, załóżmy zatem, że drugi nawias jest zero. Z założenia 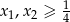x1,x2 ≥ 14 , zatem

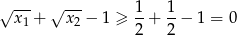
√x--+ √x--− 1 ≥ 1-+ 1− 1 = 0 1 2 2 2

i aby w tej nierówności zachodziła równość musi być 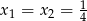x1 = x2 = 14 .

Wersja PDF