Zadanie nr 9744765
Wyznacz punkty wspólne wykresów 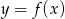 i
i 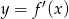 jeżeli
jeżeli 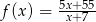 .
.
Rozwiązanie
Obliczamy pochodną funkcji 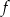 .
.
Rozwiązujemy równanie 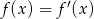 .
.
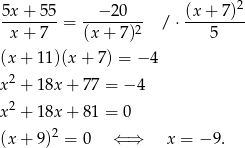
Widać więc, że wykresy przecinają się w jednym punkcie – obliczmy jeszcze jego drugą współrzędną.
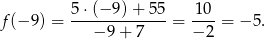
Na koniec obrazek dla ciekawskich.
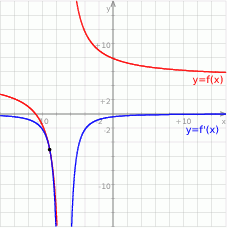
Odpowiedź: