Zadanie nr 4403236
Ze zbioru 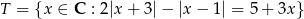 losujemy 3 liczby
losujemy 3 liczby 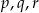 ze zwracaniem i tworzymy funkcję
ze zwracaniem i tworzymy funkcję 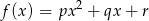 . Oblicz prawdopodobieństwa zdarzeń:
. Oblicz prawdopodobieństwa zdarzeń:
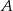 – otrzymana funkcja jest parzysta.
– otrzymana funkcja jest parzysta. 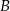 – otrzymana funkcja jest różnowartościowa.
– otrzymana funkcja jest różnowartościowa. 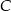 – otrzymana funkcja jest stała.
– otrzymana funkcja jest stała.
Rozwiązanie
Zacznijmy od rozszyfrowania zbioru 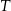 . Mamy trzy przypadki.
. Mamy trzy przypadki.
Jeżeli 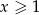 to mamy równanie
to mamy równanie
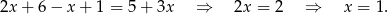
Jeżeli 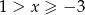 to mamy równanie
to mamy równanie
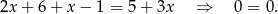
Interesują nas rozwiązania całkowite, więc mamy w tym przypadku 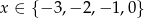 .
.
Jeżeli 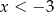 to mamy równanie
to mamy równanie
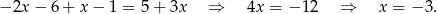
W tym przypadku nie mamy więc rozwiązań.
Zatem
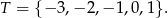
Trzy liczby z tego zbioru możemy wylosować (ze zwracaniem) na
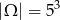
sposobów.
- Aby funkcja była parzysta musi być spełniony warunek (dla każdego
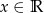 )
) 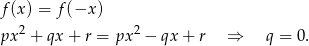
Zdarzeń sprzyjających jest więc
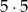 (
(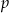 i
i  dowolne,
dowolne, 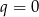 ) i prawdopodobieństwo wynosi
) i prawdopodobieństwo wynosi 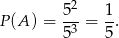
Odpowiedź: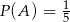
- Aby funkcja była różnowartościowa musi być liniowa, czyli
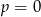 oraz nie może być stała, czyli
oraz nie może być stała, czyli 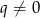 Takich trójek jest
Takich trójek jest 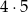 (
(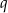 niezerowe i
niezerowe i 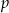 dowolne) i prawdopodobieństwo wynosi
dowolne) i prawdopodobieństwo wynosi 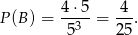
Odpowiedź: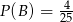
- Aby funkcja była stała, musi być
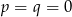 . Jest 5 takich trójek i prawdopodobieństwo wynosi
. Jest 5 takich trójek i prawdopodobieństwo wynosi 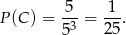
Odpowiedź: