/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Z funkcjami

Zadanie nr 6396129

Dodaj do ulubionych
Dodaj do rozwiązanych

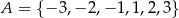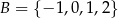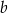Ze zbioru A = {− 3,− 2,− 1,1,2,3} losujemy liczbę a , natomiast ze zbioru B = {− 1,0,1 ,2} losujemy liczbę b . Te liczby są – odpowiednio – współczynnikiem kierunkowym i wyrazem wolnym funkcji liniowej 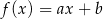f (x) = ax + b . Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymana funkcja 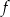f jest malejąca i ma dodatnie miejsce zerowe.

Rozwiązanie

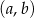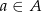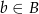Parę liczb (a,b) taką, że a ∈ A i b ∈ B możemy wybrać na

6 ⋅4 = 24

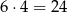
sposoby. Obliczmy teraz dla ilu par otrzymana funkcja 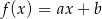f(x) = ax + b jest malejąca i ma dodatnie miejsce zerowe. Pierwszy warunek oznacza, że 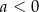a < 0 . Aby rozszyfrować drugi zauważmy, że

ax + b = 0 ⇐ ⇒ x = − b. a

Jeżeli więc 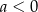a < 0 , to miejsce zerowe funkcji 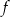f jest dodatnie wtedy i tylko wtedy, gdy 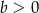b > 0 . W sumie jest więc 6 takich par:

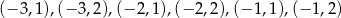
(− 3,1),(− 3,2),(− 2,1 ),(− 2,2 ),(− 1 ,1 ),(−1 ,2)

i interesujące nas prawdopodobieństwo jest równe

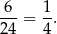
-6- 1- 24 = 4.

 
Odpowiedź: 1 4

Wersja PDF