Zadanie nr 6846142
Wzór funkcji 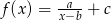 tworzymy w następujący sposób. Ze zbioru
tworzymy w następujący sposób. Ze zbioru
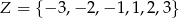
losujemy kolejno 3 liczby (bez zwracania); pierwsza z wylosowanych liczb jest równa współczynnikowi  , druga – współczynnikowi
, druga – współczynnikowi 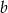 , trzecia – współczynnikowi
, trzecia – współczynnikowi  . Oblicz prawdopodobieństwo zdarzeń:
. Oblicz prawdopodobieństwo zdarzeń:
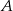 – funkcja
– funkcja 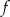 jest funkcją malejącą w każdym ze zbiorów
jest funkcją malejącą w każdym ze zbiorów 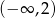 oraz
oraz 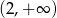 ;
; 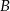 – miejscem zerowym funkcji
– miejscem zerowym funkcji 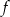 jest 0.
jest 0. 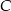 – funkcja
– funkcja 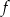 jest funkcją malejącą w każdym ze zbiorów
jest funkcją malejącą w każdym ze zbiorów 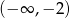 oraz
oraz 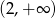 ;
;
Rozwiązanie
Na początku ustalmy, że zdarzenia elementarne to trójki wylosowanych liczb. Mamy zatem
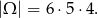
- Funkcja
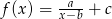 jest przesuniętą hiperbolą
jest przesuniętą hiperbolą 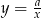 o wektor
o wektor ![[b ,c]](https://img.zadania.info/zad/6846142/HzadR3x.gif) .
. 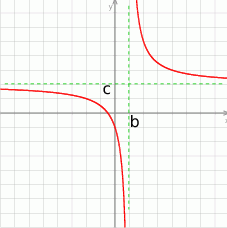
Jest ona zatem malejąca na podanych przedziałach wtedy i tylko wtedy gdy
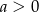 i
i 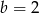 (nie może być rozerwana w żadnym z tych przedziałów, bo wtedy nie będzie malejąca).
(nie może być rozerwana w żadnym z tych przedziałów, bo wtedy nie będzie malejąca). Policzmy teraz zdarzenia sprzyjające takiej sytuacji. Liczbę
 możemy wybrać na 2 sposoby (1 lub 3). Dla liczby
możemy wybrać na 2 sposoby (1 lub 3). Dla liczby 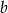 nie mamy żadnego wyboru (musimy wziąć
nie mamy żadnego wyboru (musimy wziąć 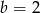 ), a liczbę
), a liczbę  możemy potem wybrać na 4 sposoby. Zdarzeń sprzyjających jest zatem
możemy potem wybrać na 4 sposoby. Zdarzeń sprzyjających jest zatem 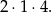
Zatem
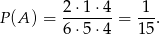
Odpowiedź: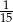
- Liczba 0 jest miejscem zerowym
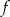 jeżeli
jeżeli 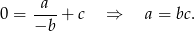
Policzmy ile jest zdarzeń sprzyjających. Jeżeli
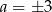 lub
lub 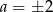 , to dla
, to dla 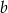 mamy 2 możliwości (np. dla
mamy 2 możliwości (np. dla 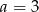 ,
, 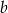 może być równe -3,-1; nie może być równe 1, bo wtedy nie da się dobrać
może być równe -3,-1; nie może być równe 1, bo wtedy nie da się dobrać  ), a liczba
), a liczba  jest jednoznacznie wyznaczona przez
jest jednoznacznie wyznaczona przez  i
i 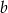 . Jeżeli
. Jeżeli 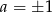 , to dla
, to dla 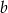 mamy tylko jedną możliwość, a
mamy tylko jedną możliwość, a  nie da się już wybrać, zatem ten przypadek nie zachodzi. Mamy zatem
nie da się już wybrać, zatem ten przypadek nie zachodzi. Mamy zatem 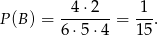
Odpowiedź: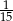
- Funkcja będzie malejąca na podanych przedziałach wtedy i tylko wtedy gdy
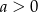 i
i 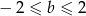 (nie może być rozerwana w żadnym z tych przedziałów, bo wtedy nie będzie malejąca).
(nie może być rozerwana w żadnym z tych przedziałów, bo wtedy nie będzie malejąca). Policzmy teraz zdarzenia sprzyjające takiej sytuacji. Liczbę
 możemy wybrać na 3 sposoby. Liczbę
możemy wybrać na 3 sposoby. Liczbę 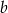 możemy potem wybrać na 4 sposoby (jeżeli
możemy potem wybrać na 4 sposoby (jeżeli 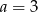 ) lub na 3 sposoby (jeżeli
) lub na 3 sposoby (jeżeli 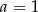 lub
lub 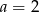 ). W każdym z przypadków mamy 4 możliwości dla liczby
). W każdym z przypadków mamy 4 możliwości dla liczby  . Zdarzeń sprzyjających jest zatem
. Zdarzeń sprzyjających jest zatem 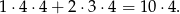
Zatem
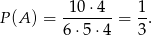
Odpowiedź: