Zadanie nr 7669726
Losujemy dwie różne liczby całkowite  i
i 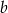 z przedziału
z przedziału 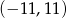 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 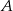 – równanie
– równanie 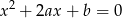 nie ma rozwiązań.
nie ma rozwiązań.
Rozwiązanie
Za zdarzenia elementarne przyjmujemy pary 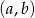 wylosowanych liczb. W przedziale
wylosowanych liczb. W przedziale 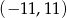 jest 21 liczb całkowitych, więc
jest 21 liczb całkowitych, więc
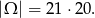
Podane równanie nie będzie miało rozwiązań jeżeli 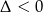 . Sprawdźmy kiedy tak jest.
. Sprawdźmy kiedy tak jest.
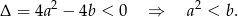
Zauważmy, że 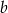 jest maksymalnie równe 10, więc musi być
jest maksymalnie równe 10, więc musi być 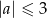 .
.
Jeżeli 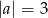 to
to 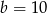 .
.
Jeżeli 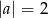 to
to 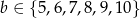 .
.
Jeżeli 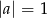 to
to 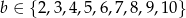
Jeżeli 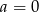 to
to 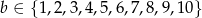 .
.
W sumie mamy więc
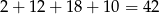
zdarzeń sprzyjających i prawdopodobieństwo wynosi
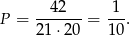
Odpowiedź: