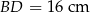/Szkoła podstawowa/Geometria/Czworokąty/Dowolny

Zadanie nr 9174072

Dodaj do ulubionych
Dodaj do rozwiązanych

Obwód czworokąta wypukłego 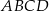ABCD jest równy 50 cm. Obwód trójkąta 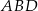ABD jest równy 46 cm, a obwód trójkąta 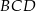BCD jest równy 36 cm. Oblicz długość przekątnej BD .

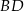Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

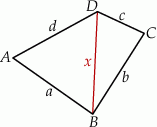
Sposób I

Przy oznaczeniach z obrazka mamy

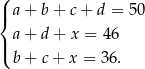
( |{ a+ b+ c + d = 50 a+ d+ x = 46 |( b+ c+ x = 36.

Dodając dwa ostatnie równania stronami i korzystając z pierwszego mamy

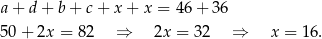
a+ d+ b+ c+ x + x = 46 + 36 50+ 2x = 8 2 ⇒ 2x = 3 2 ⇒ x = 16 .

Sposób II

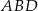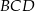Jeżeli dodamy do siebie obwody trójkątów ABD i BCD to otrzymamy obwód czworokąta 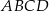ABCD oraz podwojoną długość odcinka 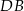DB . Zatem

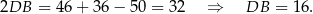
2DB = 46 + 36 − 50 = 32 ⇒ DB = 16.

 
Odpowiedź: BD = 16 cm

Wersja PDF