Zadanie nr 1392932
W pudełku są 24 kule, z czego 15 białych i 9 czarnych. Do tego pudełka dołożono pewną liczbę kul białych i trzy razy większą liczbę kul czarnych, a następnie wylosowano jedną kulę z pudełka. Prawdopodobieństwo, że wylosowana kula jest biała jest równe 0,34. Ile kul czarnych dołożono do pudełka?
Rozwiązanie
Jeżeli oznaczymy przez  liczbę kul białych dołożonych do pudełka, to kul czarnych dołożono
liczbę kul białych dołożonych do pudełka, to kul czarnych dołożono 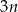 i w sumie w pudełku jest
i w sumie w pudełku jest
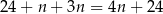
kul. Kul białych jest 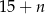 , więc otrzymujemy równanie
, więc otrzymujemy równanie
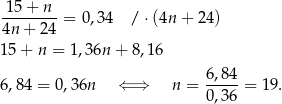
Do pudełka dołożono więc 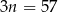 kul czarnych.
kul czarnych.
Odpowiedź: 57

