/Szkoła średnia/Prawdopodobieństwo/Z definicji/Szuflady, pudełka

Zadanie nr 2796302

Rozmieszczamy 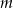m różnych listów w 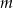m rozróżnialnych, ponumerowanych skrytkach. Jakie jest prawdopodobieństwo takiego rozmieszczenia, że dwa ustalone listy znalazły się w różnych skrytkach?

Wersja PDF

Rozwiązanie

Każdemu listowi przyporządkowujemy numer skrzynki, czyli

m |Ω | = m .

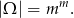
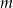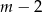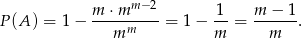
Łatwiej jest policzyć prawdopodobieństwo zdarzenia przeciwnego. Musimy policzyć na ile sposobów dwa ustalone listy wylądują w jednej skrzynce. Tę skrzynkę możemy wybrać na m sposobów. Pozostałe m − 2 listów umieszczamy zupełnie dowolnie. Daje to nam prawdopodobieństwo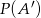

m ⋅mm −2 1 m − 1 P (A ) = 1− -----m----= 1 − --= ------. m m m

Prawdopodobieństwo P(A ′) mogliśmy też policzyć tak: ustalamy jeden list z interesującej nas pary, 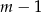m − 1 pozostałych listów umieszczamy gdzie chcemy, a ten jeden wyróżniony musimy włożyć tak, aby była para. Takich zdarzeń jest więc mm −1 .  
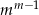Odpowiedź: m-−1 m

Wersja PDF