Zadanie nr 3135339
Do 12 ponumerowanych szuflad wkładamy losowo 13 pojedynczych skarpetek, przy czym dokładnie dwie z nich tworzą parę. Jakie jest prawdopodobieństwo otrzymania konfiguracji, w której żadna szuflada nie jest pusta oraz skarpetki tworzące parę znajdują się w różnych szufladach.
Rozwiązanie
Każdą skarpetkę możemy włożyć do jednej z 12 szuflad, więc jeżeli za zdarzenia elementarne przyjmiemy ciągi numerów szuflad, do których trafiły kolejne skarpetki to
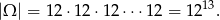
Zauważmy, że przy takim podejściu odróżniamy od siebie dwie skarpetki tworzące parę. Równie dobrze moglibyśmy uznać je za nieodróżnialne, ale nie uprościłoby to rachunków.
Zdarzenia sprzyjające policzymy na dwa sposoby, ale zanim to zrobimy zauważmy, że ponieważ skarpetek jest 13, a szuflad 12, oraz w każdej szufladzie ma być co najmniej jedna skarpetka, więc dokładnie w jednej z szuflad muszą być dwie skarpetki, a we wszystkich pozostałych po jednej skarpetce.
Sposób I
W pierwszym podejściu nie przejmujmy się skarpetkami tworzącymi parę i liczymy ile jest możliwości takich rozmieszczeń skarpetek, że żadna szuflada nie jest pusta. Liczymy następująco: wybieramy najpierw dwie skarpetki, które znajdą się w jednej szufladzie – możemy to zrobić na 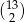 sposobów, potem wybieramy szufladę, w której się znajdą – możemy to zrobić na 12 sposobów, a na koniec dowolnie umieszczamy pozostałe 11 skarpetek w pozostałych 11 szufladach, w sumie jest więc
sposobów, potem wybieramy szufladę, w której się znajdą – możemy to zrobić na 12 sposobów, a na koniec dowolnie umieszczamy pozostałe 11 skarpetek w pozostałych 11 szufladach, w sumie jest więc
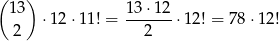
takich układów.
Teraz pozostało odjąć sytuacje, gdy dwie skarpetki z jednej pary trafiły do tej samej szuflady. Liczymy: szufladę do której trafiły możemy wybrać na 12 sposobów, a pozostałe 11 skarpetek rozmieszczamy dowolnie, czyli jest
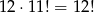
takich układów.
W takim razie jest
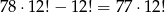
zdarzeń sprzyjających i prawdopodobieństwo wynosi
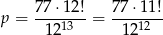
Sposób II
Tym razem policzmy od razu liczbę poprawnych układów. Mamy dwie możliwe sytuacje: albo w szufladzie, w której są dwie skarpetki nie ma żadnej skarpetki z pary, albo jedna z tych skarpetek jest skarpetką z pary.
W pierwszej sytuacji liczymy następująco: dwie skarpetki do podwójnej szuflady wybieramy spośród 11 pojedynczych skarpet, czyli na
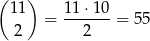
sposobów, potem ustalamy, która szuflada jest podwójna – na 12 sposobów, a na koniec dowolnie permutujemy pozostałych 11 skarpetek w pozostałych 11 szufladach. Razem jest więc
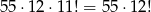
takich konfiguracji.
W drugiej sytuacji, gdy jedna ze skarpetek jest w podwójnej szufladzie, liczymy następująco: skarpetkę z pary, która ma się znaleźć w podwójnej szufladzie możemy wybrać na dwa sposoby, potem dobieramy do niej jedną pojedynczą skarpetkę – możemy to zrobić na 11 sposobów, potem ustalamy, która szuflada ma być podwójna – możemy to zrobić na 12 sposobów, a na koniec, pozostałe 11 skarpetek permutujemy dowolnie w pozostałych 11 szufladach. Łącznie jest więc
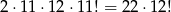
takich konfiguracji.
Mamy więc
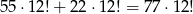
zdarzeń sprzyjających i prawdopodobieństwo wynosi
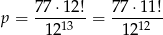
Odpowiedź: