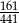Zadanie nr 4459330
W każdym z dwóch koszyków znajduje się 5 klocków czerwonych, 10 zielonych i 6 białych. Wyjmujemy losowo po jednym klocku z każdego koszyka. Oblicz prawdopodobieństwo, że:
- wylosujemy dwa klocki białe;
- wylosujemy klocki tego samego koloru.
Rozwiązanie
Powiedzmy, że zdarzenia elementarne to pary otrzymanych klocków. Zatem
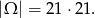
- Z każdego z koszyków możemy wybrać biały klocek na 6 sposobów. Zatem jest
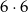
zdarzeń sprzyjających. Prawdopodobieństwo wynosi
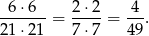
Odpowiedź: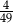
- Zdarzenia sprzyjające liczymy podobnie jak poprzednio, ale teraz mamy trzy możliwości. Zatem jest ich
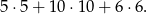
Prawdopodobieństwo wynosi
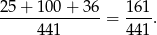
Odpowiedź: