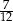/Szkoła średnia/Prawdopodobieństwo/Z definicji/Szuflady, pudełka

Zadanie nr 4593048

Dodaj do ulubionych
Dodaj do rozwiązanych

W każdym z dwóch pudełek znajduje się tyle samo kul. Kule te są w jednym z dwóch kolorów: czarne lub białe. Prawdopodobieństwo wylosowania kuli białej z pierwszego pudełka jest równe 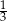13 i jest dwa razy większe niż prawdopodobieństwo wylosowania kuli czarnej z drugiego pudełka. Umieszczamy teraz wszystkie kule z tych dwóch pudełek w jednym trzecim pudełku. Jakie jest prawdopodobieństwo wylosowania kuli białej z trzeciego pudełka?

Rozwiązanie

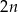Jeżeli oznaczamy przez n liczbę kul w każdym z dwóch pudełek, to w trzecim pudełku będzie 2n kul. Wiemy, że pierwszym pudełku jest 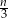n3 kul białych oraz w drugim jest 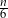n6 kul czarnych. To znaczy, że kul białych w drugim pudełku jest

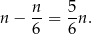
n- 5- n− 6 = 6n .

W trzecim pudełku jest więc

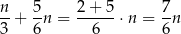
n-+ 5-n = 2-+-5-⋅n = 7n 3 6 6 6

kul białych i interesujące nas prawdopodobieństwo jest równe

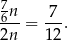
7 -6n 7-- 2n = 12.

 
Odpowiedź: -7 12

Wersja PDF