Zadanie nr 5959114
Pięć ponumerowanych kul rozmieszczamy losowo w 5 pudełkach. Jakie jest prawdopodobieństwo, że dokładnie dwa pudełka będą puste?
Rozwiązanie
Za zdarzenia elementarne przyjmijmy ciągi numerów pudełek, do których trafiają kolejne kule. Tak więc
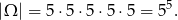
Obliczmy, ile jest zdarzeń sprzyjających. Dwa pudełka, które mają być puste możemy wybrać na
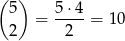
sposobów. Gdy to zrobimy pozostaje nadal 5 kul i 3 pudełka. Mamy następujące 2 możliwości: albo w jednym pudełku są trzy kule i dwóch pozostałych po jednej, albo w dwóch są po dwie kule, a w trzecim jedna. Zajmijmy się każdym z tych przypadków z osobna.
Jeżeli w jednym z pudełek mają być trzy kule, to możemy ustalić, które to pudełko na 3 sposoby, potem na
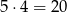
sposobów wkładamy po jednej kuli do dwóch pozostałych pudełek i na koniec pozostałe trzy kule wkładamy do wybranego wcześniej pudełka. W sumie jest więc
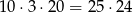
zdarzeń tego typu.
Jeżeli natomiast w jednym z pudełek ma być jedna kula, a w pozostałych po dwie, to pudełko z jedną kulą możemy wybrać na 3 sposoby, potem na 5 sposobów wybieramy kulę, która się w niej znajdzie. Następnie na
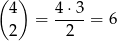
sposobów wybieramy dwie kule do następnego pudełka i na koniec pozostałe dwie kule wkładamy do ostatniego z pudełek. W sumie jest więc
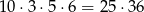
zdarzeń tego typu.
Pozostało obliczyć prawdopodobieństwo
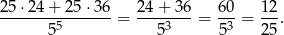
Odpowiedź: