Zadanie nr 6435035
Na stole stoją dwa identyczne koszyki, w których znajduje się po 15 jednakowej wielkości piłeczek. Piłeczki są w kolorze żółtym i czerwonym. W obu koszykach liczba piłeczek żółtych jest taka sama. Z każdego koszyka losujemy jedną piłeczkę. Ile powinno być w każdym koszyku żółtych piłeczek, aby prawdopodobieństwo wylosowania piłeczek różnych kolorów było największe?
Rozwiązanie
Powiedzmy, że w każdym z koszyków jest  żółtych piłeczek, czyli piłeczek czerwonych jest
żółtych piłeczek, czyli piłeczek czerwonych jest 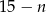 .
.
Z zdarzenia elementarne przyjmijmy pary wylosowanych piłeczek, czyli
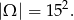
Zdarzenia sprzyjające są dwóch rodzajów: albo z pierwszego koszyka wylosowaliśmy piłeczkę żółtą, a z drugiego czerwoną, albo na odwrót. W sumie jest więc
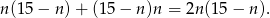
Pytanie brzmi: dla jakiego  liczba ta będzie największa? Wykresem tej funkcji jest parabola o ramionach skierowanych w dół i miejscach zerowych
liczba ta będzie największa? Wykresem tej funkcji jest parabola o ramionach skierowanych w dół i miejscach zerowych 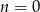 i
i 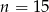 . Zatem największą wartość przyjmuje w wierzchołku, czyli dla
. Zatem największą wartość przyjmuje w wierzchołku, czyli dla 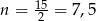 . Ponieważ liczba piłeczek musi być liczbą naturalną, największą wartość prawdopodobieństwa otrzymamy dla
. Ponieważ liczba piłeczek musi być liczbą naturalną, największą wartość prawdopodobieństwa otrzymamy dla 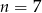 lub
lub 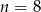 piłeczek. Można łatwo sprawdzić, że obu przypadkach otrzymamy takie samo prawdopodobieństwo (bo obie liczby są o tyle samo odległe od wierzchołka paraboli).
piłeczek. Można łatwo sprawdzić, że obu przypadkach otrzymamy takie samo prawdopodobieństwo (bo obie liczby są o tyle samo odległe od wierzchołka paraboli).
Odpowiedź: 7 lub 8

