Zadanie nr 6583253
W pojemniku umieszczono 50 drewnianych klocków, przy czym każdy klocek ma kształt sześcianu lub kuli, oraz każdy klocek jest czerwony lub niebieski. Wiadomo, że w pojemniku znajduje się dokładnie 15 czerwonych sześcianów, 18 klocków niebieskich i 31 klocków mających kształt kuli. Z pojemnika losowo wybieramy jeden klocek. Oblicz prawdopodobieństwo, że wylosowany klocek jest niebieską kulą.
Rozwiązanie
Niech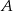 
oznacza zbiór klocków niebieskich, a 
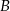zbiór klocków mających kształt kuli. Wiemy zatem, że 
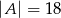i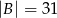 
. Zauważmy, że jeżeli klocek nie jest czerwonym sześcianem to musi on być niebieski lub musi mieć kształt kuli (być może ma obie cechy jednocześnie). Zatem
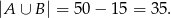
Stąd
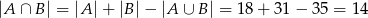
i szukane prawdopodobieństwo wynosi
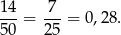
Odpowiedź: 
