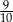Zadanie nr 8046271
W pojemniku znajdują się dwie kule białe i trzy czerwone. Losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę czerwoną. Wynik przedstaw w postaci ułamka nieskracalnego.
Rozwiązanie
Sposób I
Za zdarzenia elementarne przyjmijmy pary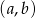 
wylosowanych kul. Pierwszą kulę możemy wybrać na 5 sposobów, a drugą na 4. Zatem
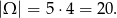
Zamiast obliczać liczbę zdarzeń sprzyjających zdarzeniu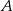 
polegającym na wybraniu co najmniej jednej kuli czerwonej, zauważmy, że łatwo jest obliczyć liczbę zdarzeń przeciwnych do 
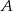– są to zdarzenia, w których obie kule są białe. Są dwa takie zdarzenia (bo umówiliśmy się, żeby uwzględniać kolejność w wybieranych parach). Zatem
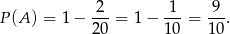
Sposób II
Tym razem za zdarzenia sprzyjające przyjmijmy nieuporządkowane pary (zbiory)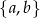 
wylosowanych kul. Mamy więc
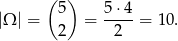
Podobnie jak w poprzednim sposobie zauważamy teraz, że jest dokładnie jedno zdarzenie, w którym obie wylosowane kule są białe (jest jedno zdarzenie, bo teraz nie uwzględniamy kolejności). Interesujące nas prawdopodobieństwo jest więc równe
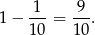
Odpowiedź: 
