Zadanie nr 9284778
Listonosz losowo rozmieszcza 7 listów w 5 różnych skrzynkach na listy. Oblicz prawdopodobieństwo, że w każdej skrzynce znajdzie się przynajmniej jeden list.
Rozwiązanie
O zdarzeniach elementarnych myślimy jak o ciągach numerów skrzynek, do których trafiły kolejne listy. Mamy zatem
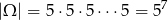
(każdy list może trafić do jednej z pięciu skrzynek).
W zdarzeniach sprzyjających mamy dwie możliwości: albo w jednej ze skrzynek są trzy listy, a w każdej z pozostałych po jednym liście, albo też w dwóch skrzynkach są dwa listy, a we wszystkich pozostałych po jednym liście. Policzmy osobno liczbę zdarzeń w każdym z tych przypadków.
Sposób I
Załóżmy, że w jednej ze skrzynek są trzy listy. Skrzynkę tę możemy wybrać na 5 sposobów. Ponadto mamy
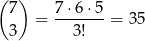
możliwości wyboru trzech listów, które będą w tej skrzynce. Pozostałe 4 listy umieszczamy w pozostałych 4 skrzynkach, tak, aby w każdej skrzynce był jeden list – można to zrobić na 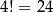 sposoby. W sumie jest więc
sposoby. W sumie jest więc
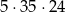
ciągów, w których trzy listy znalazły się w jednej skrzynce.
Zajmijmy się teraz sytuacją, gdy są dwie skrzynki zawierające dwa listy. Dwie skrzynki możemy wybrać na
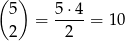
sposobów. Potem wybieramy 4 listy, które znajdą się w tych skrzynkach. Możemy to zrobić na
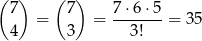
sposobów. Musimy jeszcze ustalić, które dwa z tych czterech listów trafią do pierwszej z wybranych skrzynek. Możemy to zrobić na
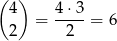
sposobów. (Cztery listy, które mają trafić do dwóch wyróżnionych skrzynek mogliśmy też wybrać inaczej: najpierw dwa do pierwszej skrzynki na 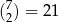 sposobów, a potem dwa do drugiej na
sposobów, a potem dwa do drugiej na 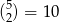 sposobów.)
sposobów.)
Na koniec pozostałe 3 listy dowolnie permutujemy pomiędzy 3 pozostałymi skrzynkami. W tym przypadku jest więc
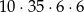
możliwości.
Szukane prawdopodobieństwo jest więc równe
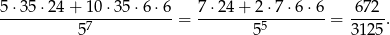
Sposób II
Załóżmy, że w jednej ze skrzynek są trzy listy. Skrzynkę tę możemy wybrać na 5 sposobów. Teraz umieszczamy listy w skrzynkach. Najpierw wkładamy listy do skrzynek, w których ma być jeden list: do pierwszej wkładamy jeden z 7 listów, do drugiej jeden z 6 pozostałych, do trzeciej jeden z 5 i do czwartej jeden z 4. Przy ostatniej skrzynce (w której mają być 3 listy) nie mamy już wyboru i wkładamy do niej pozostałe 3 listy. Jest więc
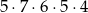
ciągów, w których trzy listy znalazły się w jednej skrzynce.
Zajmijmy się teraz sytuacją, gdy są dwie skrzynki zawierające dwa listy. Dwie skrzynki możemy wybrać na
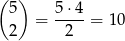
sposobów. Teraz wkładamy do skrzynek listy. Tak jak poprzednio, najpierw wkładamy listy do skrzynek, w których ma być jeden list – możemy to zrobić na
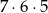
sposobów. Teraz z pozostałych 4 listów musimy wybrać dwa, które trafią do kolejnej skrzynki (w której mają być dwa listy). Możemy to zrobić na
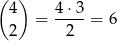
sposobów. Na koniec wkładamy pozostałe dwa listy do ostatniej skrzynki. W sumie jest więc
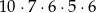
ciągów, w których w dwóch skrzynkach są dwa listy.
Szukane prawdopodobieństwo jest więc równe
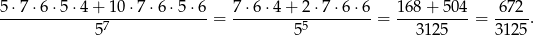
Odpowiedź: