Zadanie nr 1332090
Oblicz, ile jest wszystkich liczb dziewięciocyfrowych, w zapisie których dokładnie trzy razy występuje siódemka, dokładnie dwa razy czwórka, a pozostałe cyfry nie mogą się powtarzać i żadna cyfra nie jest zerem.
Rozwiązanie
Liczymy ile jest takich liczb.
Miejsca dla trzech siódemek można wybrać na
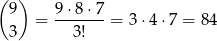
sposoby.
Jeżeli mamy już umieszczone siódemki, to miejsca dla dwóch czwórek możemy wybrać na
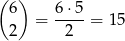
sposobów.
Na pozostałych 4 miejscach różne cyfry możemy umieścić na
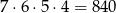
sposobów.
W sumie jest więc
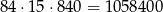
takich liczb.
Odpowiedź: 1 058 400

