/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 1590275

Dodaj do ulubionych
Dodaj do rozwiązanych

Ile jest liczb naturalnych czterocyfrowych, w których żadne dwie spośród cyfr: 1,3,5,7,9 nie sąsiadują ze sobą?

Rozwiązanie

Zastanówmy się ile może być cyfr nieparzystych w takiej liczbie?

Może nie być żadnej – jest

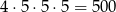
4 ⋅5⋅5 ⋅5 = 500

takich liczb (pierwsza cyfra nie może być zerem, pozostałe to dowolne cyfry parzyste).

Jeżeli jest jedna cyfra nieparzysta to może znajdować się na początku – jest

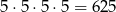
5 ⋅5⋅5 ⋅5 = 625

takich liczb (wybieramy dowolną cyfrę nieparzystą na pierwszym miejscu i dowolne cyfry parzyste na pozostałych). Jeżeli natomiast cyfra nieparzysta jest na jednym z 3 pozostałych miejsc to mamy

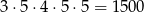
3 ⋅5⋅ 4⋅5 ⋅5 = 15 00

możliwości (wybieramy miejsce cyfry nieparzystej, wybieramy cyfrę nieparzystą, wybieramy pierwszą cyfrę parzystą niezerową i w końcu wybieramy dwie cyfry parzyste na pozostałe miejsca).

Jeżeli są dwie cyfry nieparzyste i jedna z nich jest pierwszą cyfrą to mamy

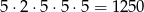
5 ⋅2⋅ 5⋅5 ⋅5 = 12 50

możliwości (wybieramy pierwszą cyfrę nieparzystą, ustalamy gdzie ma być druga cyfra nieparzysta – na trzecim, czy czwartym miejscu, wybieramy tę cyfrę nieparzystą i na koniec wybieramy dwie pozostałe cyfry parzyste).

Jeżeli są dwie cyfry nieparzyste i żadna z nich nie stoi na pierwszym miejscu to muszą one być na miejscach drugim i czwartym, co daje

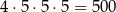
4 ⋅5⋅5 ⋅5 = 500

możliwości (pierwsza cyfra musi być niezerowa).

W sumie jest więc

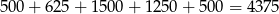
500 + 625 + 15 00+ 1250 + 500 = 4375

liczb spełniających warunki zadania.  
Odpowiedź: 4375

Wersja PDF