/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 1868291

Na ile sposobów można wybrać ze zbioru 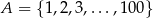A = {1 ,2,3,...,100} trzy różne liczby, których suma przy dzieleniu przez 3 daje resztę 1.

Wersja PDF

Rozwiązanie

W danym zbiorze są 33 liczby:

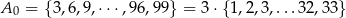
A 0 = {3,6 ,9 ,⋅⋅⋅,96,99} = 3⋅ {1,2,3,...32,33 }

podzielne przez 3. Są 34 liczby:

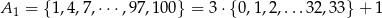
A1 = { 1,4,7,⋅⋅⋅,97 ,100} = 3 ⋅{0 ,1 ,2,...32,33} + 1

które przy dzieleniu przez 3 dają resztę 1, oraz 33 liczby:

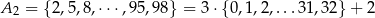
A 2 = {2,5 ,8,⋅⋅⋅,95,98} = 3⋅ {0,1,2,...31,32 }+ 2

które przy dzieleniu przez 3 dają resztę 2. Powiedzmy, że wybraliśmy trzy liczby 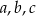a,b,c ze zbioru 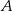A . Jeżeli suma tych liczb ma dawać resztę 1 przy dzieleniu przez 3, to musi zachodzić jeden z przypadków:
1. Dwie z tych liczb dzielą się przez 3, a jedna daje resztę jeden przy dzieleniu przez 3. Takie trzy liczby możemy wybrać na

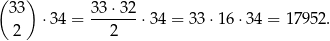
( ) 33 ⋅34 = 33-⋅32-⋅34 = 3 3⋅1 6⋅34 = 17952. 2 2

sposoby.
2. Jedna liczba dzieli się przez 3, a dwie pozostałe dają resztę 2 przy dzieleniu przez 3. Takie trzy liczby możemy wybrać na

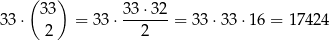
( ) 33 ⋅ 33 = 33 ⋅ 33-⋅32-= 33⋅ 33⋅ 16 = 1742 4 2 2

sposoby.
3. Jedna liczba daję resztę 2, a dwie pozostałe resztę 1 przy dzieleniu przez 3. Takie trzy liczby możemy wybrać na

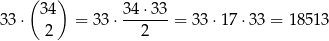
( ) 34 34 ⋅33 33 ⋅ 2 = 33 ⋅---2---= 33⋅ 17⋅ 33 = 1851 3

sposoby.

W sumie jest więc

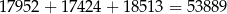
179 52+ 17424 + 185 13 = 5388 9

możliwości wybrania trzech liczb spełniających warunki zadania.  
Odpowiedź: 53889

Wersja PDF