Zadanie nr 1871676
Oblicz, ile jest czterocyfrowych liczb naturalnych parzystych, w których występuje dokładnie jedno zero.
Rozwiązanie
Liczymy na ile sposobów można utworzyć liczbę spełniającą warunki zadania.
Jeżeli ostatnią cyfrą takiej liczby jest zero, to każdą z pozostałych cyfr możemy wybrać na 9 sposobów, więc jest
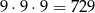
liczb tej postaci.
Jeżeli ostatnia, cyfra nie jest zerem, to możemy ją wybrać na 4 sposoby (musi być niezerowa i parzysta), pierwszą na 9 sposobów, potem na jednym z dwóch pozostałych miejsc umieszczamy zero i na koniec na pozostałym miejscu umieszczamy jedną z 9 liczb niezerowych. Jest więc
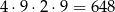
liczb tej postaci. W sumie jest więc
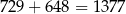
liczb spełniających warunki zadania.
Odpowiedź: 1377

