/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 2049659

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru 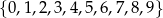{0,1,2,3,4,5,6 ,7 ,8,9} losujemy kolejno 4 cyfry bez zwracania, a następnie zapisujemy je w kolejności losowania tworząc liczbę 4 cyfrową. Ile można otrzymać w ten sposób

  • dowolnych liczb?
  • liczb podzielnych przez 25?

Rozwiązanie

  • Pierwszą cyfrę możemy wylosować na 9 sposobów (bo nie może być 0), wtedy dla drugiej mamy też 9 możliwości, dla trzeciej 8, a dla czwartej 7. Razem jest więc
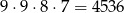
    9 ⋅9⋅8 ⋅7 = 4536

    możliwości.  
    Odpowiedź: 4536

  • Liczba dzieli się przez 25, jeżeli jej dwie ostatnie cyfry to 00, 25, 50 lub 75. Pierwsza możliwość odpada, bo losujemy bez zwracania. Jeżeli końcówką jest 50, to pozostałe dwie cyfry możemy wybrać na 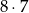8⋅7 sposobów. Jeżeli natomiast końcówką jest 25 lub 75, to mamy 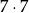7⋅7 sposobów (nie może być 0 na początku). W sumie daje nam to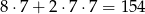
    8⋅7 + 2 ⋅7 ⋅7 = 154

    możliwości.  
    Odpowiedź: 154

Wersja PDF