Zadanie nr 2061401
Oblicz, ile jest liczb naturalnych trzycyfrowych, które są podzielne przez 5, i których zapis składa się z 3 różnych cyfr.
Rozwiązanie
Jeżeli liczba ma być podzielna przez 5, to jej ostatnią cyfrą musi być 0 lub 5. Policzmy osobno te sytuacje.
Jeżeli na końcu jest 5, to pierwszą cyfrę możemy wybrać na 8 sposobów (nie może być ani 5, ani 0). Drugą cyfrę też możemy wybrać na 8 sposobów (musi być różna od pierwszej i ostatniej cyfry). Łącznie daje to
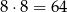
liczby.
Jeżeli natomiast na końcu jest 0, to pierwszą cyfrę możemy wybrać na 9 sposobów (nie może być 0), a drugą na 8 sposobów (musi być różna od pierwszej i ostatniej cyfry). Razem daje to
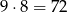
liczby.
W sumie jest więc
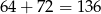
liczb spełniających warunki zadania.
Odpowiedź: 136

