/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 2774345

Rozważamy wszystkie liczby naturalne pięciocyfrowe zapisane przy użyciu cyfr 4, 5, 6, 7, 8 bez powtarzania jakiejkolwiek cyfry. Oblicz sumę wszystkich takich liczb.

Wersja PDF

Rozwiązanie

Zauważmy najpierw, że suma jedności wszystkich takich liczb będzie równa

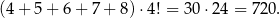
(4+ 5 + 6 + 7 + 8) ⋅4! = 30 ⋅24 = 7 20.

Tak jest, bo każda z cyfr pojawi się dokładnie w 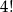4! liczb jako cyfra jedności.

Analogicznie, suma wszystkich dziesiątek utworzonych liczb będzie równa

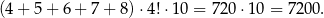
(4 + 5 + 6 + 7 + 8) ⋅4!⋅1 0 = 720 ⋅10 = 72 00.

I tak dalej dla kolejnych cyfr. Interesująca nas suma jest więc równa

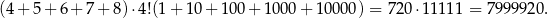
(4+ 5 + 6 + 7+ 8)⋅4!(1+ 10+ 10 0+ 10 00+ 1 0000) = 72 0⋅111 11 = 7999 920

 
Odpowiedź: 7999920

Wersja PDF