Zadanie nr 2940708
Z cyfr 0, 1, 2 tworzymy pięciocyfrowe liczby całkowite dodatnie podzielne przez 15. Oblicz, ile możemy utworzyć takich liczb.
Rozwiązanie
Oczywiście ostatnią cyfrą utworzonej liczby musi być 0. Pozostało więc wybrać pierwsze 4 cyfry tak, aby ich suma dzieliła się przez 3 (bo wtedy cała liczba będzie się dzielić przez 3). Te 4 cyfry mogą być równe (na razie nie zwracamy uwagi na ich kolejność):
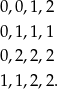
Obliczymy kolejno, ile jest możliwości utworzenia liczb o takich cyfrach. W pierwszym przypadku jest
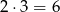
takich liczb (na dwa sposoby wybieramy pierwszą niezerową cyfrę i umieszczamy ją na początku tworzonej liczby, potem na 3 sposoby możemy umieścić drugą niezerową cyfrę, na koniec na pozostałych dwóch miejscach umieszczamy zera).
Są 3 liczby drugiego i 3 liczby trzeciego rodzaju (w każdym z tych przypadków na 3 sposoby możemy umieścić 0).
Jeżeli chodzi o ostatnią możliwość, to jest
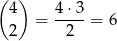
takich liczb (ustalamy miejsca dla jedynek i na pozostałych dwóch miejscach umieszczamy dwójki).
W sumie jest więc
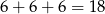
liczb spełniających warunki zadania.
Odpowiedź: 18

