/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 3075926

Dodaj do ulubionych
Dodaj do rozwiązanych

Ile jest liczb naturalnych ośmiocyfrowych, których suma cyfr jest równa 4?

Rozwiązanie

Sposób I

Zastanówmy się jaka może być największa cyfra liczby ośmiocyfrowej o sumie cyfr równej 4?

Oczywiście żadna cyfra nie może być większa od 4 i jeżeli jedną z cyfr jest 4, to wszystkie pozostałe cyfry muszą być zerami. Jest tylko jedna taka liczba: 40000000.

Jeżeli największą cyfrą jest 3, to musi być jeszcze jedna jedynka i reszta to same zera. Policzmy ile jest takich liczb. Pierwszą cyfrę możemy wybrać na dwa sposoby (może to być 3 lub 1), a drugą niezerową cyfrę możemy umieścić na jednej z 7 pozostałych pozycji. Jest więc

2 ⋅7 = 14

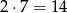
takich liczb.

Jeżeli największą cyfrą jest 2, to mamy dwie możliwości: albo są dwie dwójki, albo jedna dwójka i dwie jedynki. Jest 7 liczb z dwoma dwójkami (pierwsza musi stać na początku, a druga na jednym z pozostałych 7 miejsc). Policzmy ile jest liczb z jedną dwójką i dwoma jedynkami. Jeżeli dwójka jest na początku, to pozostałe dwie jedynki możemy umieścić na

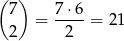
( ) 7 7 ⋅6 = ---- = 2 1 2 2

sposobów, jest więc 21 takich liczb. Jeżeli na początku jest jedynka, to możliwych liczb jest

7 ⋅6 = 42

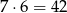
(wybieramy miejsce dla jedynki i potem dla dwójki).

Ostatnia możliwość to liczby składające się z czterech jedynek i czterech zer. Jedna jedynka musi być pierwszą cyfrą, a pozostałe 3 możemy umieścić na

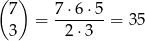
( 7) 7⋅ 6⋅5 = -------= 35 3 2 ⋅3

sposobów.

W sumie jest więc

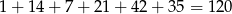
1 + 14 + 7 + 21 + 42 + 35 = 120

liczb spełniających warunki zadania.

Sposób II

Tym razem będziemy trochę sprytniejsi. Zauważmy, że każdą liczbę ośmiocyfrową o sumie liczby równej 4 możemy zakodować przy pomocy 4 kropek i 9 pionowych kresek, np. liczbę 10021000 może zakodować w postaci

|⋅|||⋅⋅|⋅||||

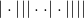
(Pionowe kreski oddzielają kolejne cyfry liczby, a liczb kropek mówi nam o tym, ile jest równa dana cyfra.) Zauważmy, że przy takim sposobie kodowania mamy 10 ruchomych symboli (kresek i kropek). Tak jest, bo wszystkich symboli jest 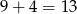9 + 4 = 1 3 , ale skrajne kreski (oznaczające początek i koniec liczby) oraz pierwsza od lewej kropka nie mogą zmienić swojej pozycji (bo pierwsza cyfra liczby nie może być zerem). Pozostałe 10 symboli możemy natomiast rozmieszczać dowolnie i różne układy odpowiadają różnym liczbom.

Pozostało więc obliczyć, ile jest różnych układów 7 kresek i 3 kropek. To jest jednak łatwe: wystarczy wybrać miejsca dla 3 kropek. Jest więc

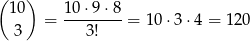
( ) 10 10⋅-9⋅8- 3 = 3! = 10 ⋅3⋅ 4 = 120

takich układów. Tyle samo jest interesujących nas liczb.  
Odpowiedź: 120

Wersja PDF