Zadanie nr 3193718
Oblicz, ile jest wszystkich liczb naturalnych pięciocyfrowych nieparzystych, w których zapisie występują co najmniej trzy jedynki.
Rozwiązanie
Wszystkich liczb nieparzystych pięciocyfrowych jest
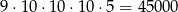
(na początku nie może być 0). Wśród nich jest 1 składająca się z samych jedynek.
Sposób I
Zastanówmy się, ile jest liczb zawierających 4 jedynki? Jeżeli cyfra, która nie jest jedynką jest na końcu, to są 4 takie liczby (wybieramy ostatnią cyfrę, która musi być nieparzysta i nie może być jedyną). Jeżeli cyfra, która nie jest jedynką jest na początku, to jest 8 takich liczb (wybieramy pierwszą cyfrę, która nie może być zerem ani jedynką). Jeżeli wreszcie cyfra, która nie jest jedynką nie jest ani na końcu, ani na początku, to jej miejsce możemy wybrać na 3 sposoby, a samą cyfrę na 9 sposobów, więc jest 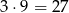 takich liczb. W sumie jest więc
takich liczb. W sumie jest więc
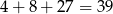
liczb z czterema jedynkami.
Obliczamy teraz, ile jest liczb z trzema jedynkami. Jeżeli jedynki są na początku i na końcu, to na 3 sposoby wybieramy miejsce dla trzeciej jedynki i na  sposobów dobieramy dwie pozostałe cyfry. Są więc
sposobów dobieramy dwie pozostałe cyfry. Są więc
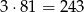
takie liczby. Jeżeli jedynka jest na końcu, ale nie na początku, to na 8 sposobów wybieramy pierwszą cyfrę, na 3 sposoby wybieramy miejsce drugiej cyfry, która nie jest jedynką i na 9 sposobów wybieramy tę cyfrę. Jest więc
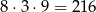
takich liczb. Jeżeli jedynka jest na początku, ale nie na końcu, to ostatnią cyfrę wybieramy na 4 sposoby, na 3 sposoby wybieramy miejsce drugiej cyfry, która nie jest jedynką i na 9 sposobów wybieramy tę cyfrę. Jest więc
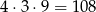
takich liczb. Jeżeli wreszcie nie ma jedynki ani na początku, ani na końcu, to wybieramy tylko na 4 sposoby ostatnią cyfrę i na 8 sposobów pierwszą. Są więc
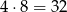
takie liczby.
W sumie jest więc
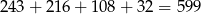
liczb z trzema jedynkami.
Liczb spełniających warunki zadania jest więc
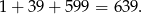
Sposób II
Tym razem obliczenia wykonamy trochę ’na około’, tzn. obliczymy ile jest liczb, które nie spełniają warunków zadania.
Liczb nieparzystych, w których nie ma żadnej jedynki jest
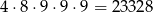
(wybieramy najpierw ostatnią cyfrę, która musi być liczbą nieparzystą, potem wybieramy pierwszą cyfrę, która nie może być zerem, a pozostałe 3 cyfry wybieramy dowolnie – w każdym kroku pamiętamy o tym, że nie możemy wybrać jedynki).
Obliczmy teraz, ile jest liczb z jedną jedynką. Są w tym przypadku trzy różne sytuacje. Jeżeli jedynka jest ostatnią cyfrą, to możemy dobrać do niej pozostałe cyfry na
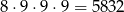
sposoby (nie może być jedynki i na początku nie może być zero). Jeżeli jedynka jest na początku, to pozostałe cyfry możemy dobrać na
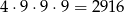
sposobów. Jeżeli wreszcie jedynka nie jest ani na początku, ani na końcu, to jej miejsce możemy wybrać na 3 sposoby, a pozostałe cyfry możemy dobrać na 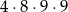 sposoby. Jest więc
sposoby. Jest więc
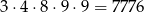
liczb z jedynką w środku.
W sumie mamy więc
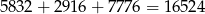
liczb z jedną jedynką.
Zajmijmy się teraz liczbami z dwoma jedynkami. Jeżeli jedynki są na początku i na końcu, to pozostałe 3 cyfry możemy wybrać na
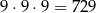
sposobów. Jeżeli jedynka jest na końcu, ale nie na początku, to miejsce drugiej jedynki możemy wybrać na 3 sposoby, a pozostałe cyfry dobieramy na 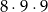 sposobów, więc są
sposobów, więc są
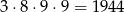
takie liczby. Jeżeli jedynka jest na początku, ale nie na końcu, to miejsce drugiej jedynki możemy wybrać na 3 sposoby, a pozostałe cyfry dobieramy na 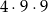 sposobów, więc są
sposobów, więc są
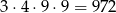
takie liczby. Jeżeli wreszcie nie ma jedynki ani na początku, ani na końcu, to miejsca dla jedynek możemy wybrać na 3 sposoby, a pozostałe cyfry dobieramy na 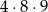 sposobów, więc są
sposobów, więc są
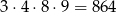
takie liczby.
W sumie jest więc
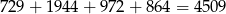
liczb z dwoma jedynkami.
Liczb spełniających warunki zadania jest więc
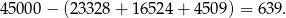
Odpowiedź: 639

