/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 3487050

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru liczb 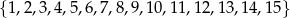{1,2 ,3 ,4,5,6,7,8,9,10,1 1,12,13,14,15 } losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę 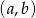(a ,b) , gdzie a jest wynikiem pierwszego losowania, 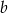b jest wynikiem drugiego losowania. Oblicz, ile jest wszystkich par 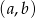(a,b) takich, że iloczyn 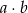a ⋅b jest liczbą parzystą.

Rozwiązanie

Sposób I

Są dwa rodzaje par 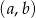(a,b) , dla których 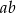ab jest liczbą parzystą: pary, w których obie liczby są parzyste – takich par jest

7 ⋅6 = 42

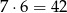
(pierwszą liczbę wybieramy na 7 sposobów, a drugą na 6 sposobów), oraz takie, w których tylko jedna liczba jest parzysta – takich par jest

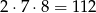
2 ⋅7 ⋅8 = 112

(na 2 sposoby wybieramy, która liczba ma być parzysta, potem wybieramy tę liczbę parzystą, a na koniec dobieramy do niej liczbę nieparzystą).

W sumie są więc

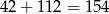
4 2+ 1 12 = 154

interesujące nas pary.

Sposób II

Tym razem obliczmy, ile jest par, które nie spełniają warunków zadania. W takich parach obie liczby muszą być nieparzyste, więc jest ich

8 ⋅7 = 56.

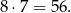
W takim razie wszystkich par z parzystym iloczynem jest

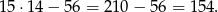
15 ⋅14 − 56 = 21 0− 56 = 154.

 
Odpowiedź: 154

Wersja PDF