/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 3524847

Dodaj do ulubionych
Dodaj do rozwiązanych

Cyfry 0, 1, 2, 3, 4, 5, 6 ustawiamy losowo w liczbę siedmiocyfrową o różnych cyfrach. Ile jest możliwych ustawień, w których otrzymamy liczbę siedmiocyfrową

  • podzielną przez 4
  • parzystą.

Rozwiązanie

  • Liczba dzieli się przez cztery, jeżeli liczba utworzona z jej dwóch ostatnich cyfr dzieli się przez 4. Pozostałe cyfry nie mają znaczenia. Jeżeli w tej końcówce jest zero, czyli jest to jedna z końcówek
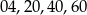
    04,20,40,60

    to pozostałe 5 cyfr możemy ustawić zupełnie dowolnie, czyli w tym przypadku mamy

    4 ⋅5!

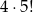
    możliwości.

    Jeżeli natomiast w końcówce nie ma zera, czyli jest to jedna z końcówek

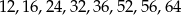
    12,16 ,24,32,36,52 ,56,64

    na pierwszą cyfrę możemy wybrać na 4 sposoby (bo nie może być 0), a pozostałe dowolnie, czyli w sumie mamy

    8⋅4 ⋅4!.

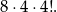
    Razem mamy więc

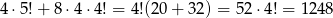
    4⋅5 !+ 8 ⋅4⋅ 4! = 4!(2 0+ 3 2) = 52 ⋅4! = 1248

    możliwości.  
    Odpowiedź: 1248

  • Liczymy podobnie jak poprzednio, ale teraz patrzymy tylko na ostatnią cyfrę. Jeżeli jest to 0, to mamy
    6!

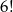
    możliwości, a jeżeli jest to parzysta liczba niezerowa (czyli 2,4 lub 6), to mamy

    3⋅ 5⋅5 !

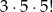
    możliwości (pierwszą cyfrę możemy wybrać na 5 sposobów, pozostałe ustawiamy dowolnie). Razem daje to nam

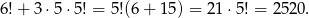
    6 !+ 3 ⋅5⋅5 ! = 5!(6 + 15 ) = 21⋅ 5! = 2520.

     
    Odpowiedź: 2520

Wersja PDF