Zadanie nr 3599508
Oblicz, ile jest wszystkich liczb naturalnych pięciocyfrowych, w których zapisie występują dokładnie trzy cyfry nieparzyste.
Rozwiązanie
Miejsca dla trzech cyfr nieparzystych możemy wybrać na 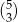 sposoby, ale musimy być trochę ostrożniejsi, bo pierwszą cyfrą nie może być 0.
sposoby, ale musimy być trochę ostrożniejsi, bo pierwszą cyfrą nie może być 0.
Sposób I
Jeżeli pierwsza (najbardziej znacząca) cyfra liczby jest parzysta, to możemy ją wybrać na 4 sposoby (nie może być 0). Potem na
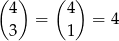
sposoby wybieramy miejsca dla cyfr nieparzystych i każdą z 4 cyfr wybieramy na 5 sposobów. W sumie jest więc
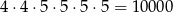
takich liczb.
Jeżeli pierwsza cyfra jest nieparzysta, to możemy ją wybrać na 5 sposobów. Potem na
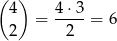
sposobów wybieramy miejsca dla pozostałych cyfr nieparzystych i każdą z 4 cyfr wybieramy na 5 sposobów. W sumie jest więc
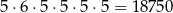
takich liczb.
Wszystkich możliwości jest więc
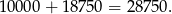
Sposób II
Zauważmy, że jeżeli dokładnie trzy cyfry są nieparzyste, to dokładnie dwie są parzyste.
Jeżeli pierwszą cyfrą utworzonej liczby jest liczba nieparzysta, to możemy ją wybrać na 5 sposobów. Wśród pozostałych cyfr mają być dwie cyfry parzyste – ich miejsce możemy wybrać na
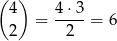
sposobów. Gdy już to ustalimy, każdą z pozostałych 4 cyfr możemy wybrać na 5 sposobów. W sumie jest więc
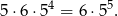
takich liczb.
Jeżeli natomiast pierwsza cyfra jest parzysta, to możemy ją wybrać na 4 sposoby. Potem musimy jeszcze ustalić, gdzie ma być druga cyfra parzysta – możemy to zrobić na 4 sposoby. Gdy już to ustalimy, każdą z pozostałych 4 cyfr możemy wybrać na 5 sposobów. W sumie jest więc
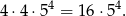
takich liczb.
Wszystkich liczb spełniających warunki zadania jest więc
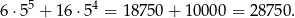
Sposób III
Wszystkich ciągów cyfr długości 5, w których są 3 cyfry nieparzyste jest
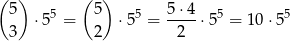
(wybieramy miejsca dla cyfr nieparzystych a potem każdą cyfrę wybieramy na 5 sposobów). Wśród tych ciągów jest
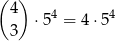
ciągów, które zaczynają się zerem. W takim razie jest
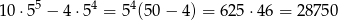
liczb spełniających warunki zadania.
Odpowiedź: 28750

