/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 4027935

Dodaj do ulubionych
Dodaj do rozwiązanych

W pewnym budynku biurowym przydzielono pracownikom pięciocyfrowe kody bezpieczeństwa, przy czym każdy kod musiał spełniać następujące dwa warunki:
(1) kod musi zawierać co najmniej 3 różne cyfry
(2) kod musi zawierać co najmniej jedną cyfrę parzystą i co najmniej jedną cyfrę nieparzystą.
Ile jest kodów spełniających powyższe warunki?

Rozwiązanie

Zamiast liczyć ile jest ’dobrych’ kodów, policzmy ile jest ’złych’.

Jest

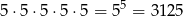
5 ⋅5 ⋅5⋅ 5⋅5 = 55 = 3125

kodów, w których wszystkie cyfry są parzyste i tyle samo kodów, w których wszystkie cyfry są nieparzyste. Zatem warunek (2) eliminuje

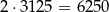
2 ⋅312 5 = 6250

kodów.

Zastanówmy się teraz nad warunkiem (1).

Nie ma już kodów składających się z jednej cyfry, bo w takich kodach wszystkie cyfry są albo parzyste, albo nieparzyste, a takie kody już odjęliśmy.

Policzmy ile jest kodów, w których są dokładnie dwie różne cyfry (i jedna parzysta, a druga nieparzysta). Każdy taki kod musi mieć jedną z postaci:

aaaab ,aaaba,aabaa ,abaaa,baaaa aaabb ,aabab,abaab ,baaab, aabba ,ababa,baaba , abbaa ,babaa, bbaaa .

W każdej z powyższych konfiguracji a możemy wybrać na 10 sposobów, a 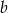b na 5 sposobów (bo 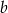b musi mieć inną parzystość niż a ). W sumie jest więc

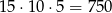
15 ⋅10 ⋅5 = 75 0

takich kodów.

Wszystkich kodów pięciocyfrowych jest

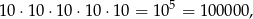
10⋅1 0⋅10 ⋅10 ⋅10 = 105 = 1000 00,

więc kodów spełniających warunki (1)-(2) jest

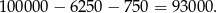
1000 00− 6250 − 750 = 93000.

 
Odpowiedź: 93 000

Wersja PDF