Zadanie nr 4034054
Oblicz, ile jest wszystkich liczb naturalnych sześciocyfrowych, w których zapisie występują co najmniej trzy cyfry nieparzyste.
Rozwiązanie
Łatwiej będzie obliczyć ile jest liczb sześciocyfrowych, które nie spełniają warunku podanego w treści zadania, tzn. takich, w których zapisie występują 0, 1 lub 2 cyfry nieparzyste.
Wszystkich liczb sześciocyfrowych jest
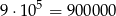
i wśród nich jest
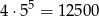
liczb o wszystkich cyfrach parzystych (pierwsza cyfra nie może być zerem, więc możemy ją wybrać na 4 sposoby, a pozostałe cyfry na 5 sposobów).
Jeżeli jedna cyfra ma być nieparzysta, to albo jest na początku i wtedy mamy
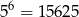
możliwości wybrania cyfr takiej liczby, albo nie jest na początku i wtedy możemy taką liczbę wybrać na
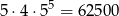
sposoby (na 5 sposobów wybieramy miejsce cyfry nieparzystej, potem na 4 sposoby pierwszą cyfrę i na koniec każdą z pozostałych cyfr możemy wybrać na 5 sposobów).
Pozostało się teraz zająć liczbami, w których są 2 cyfry nieparzyste. Jeżeli jedna z nich jest na początku utworzonej liczby, to możemy taką liczbę utworzyć na
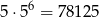
sposobów (na 5 sposobów wybieramy miejsce drugiej liczby nieparzystej i potem każdą z cyfr możemy wybrać na 5 sposobów). Jeżeli natomiast żadna z cyfr nieparzystych nie jest na początku, to ich miejsca możemy wybrać na
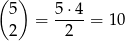
sposobów. Jest więc
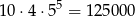
takich liczb (pierwszą cyfrę możemy wybrać na 4 sposoby, a każdą pozostałą cyfrę na 5 sposobów).
W sumie jest więc
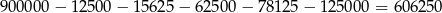
liczb spełniających warunki zadania.
Odpowiedź: 606 250

